CS 294-2, Visual Grouping and Object Recognition (Prof. Jitendra malik) Sep. 29, 1999
Lecture 10 Normalized Cuts and Orientation Energy, DRAFT notes by Ganping Sun
---------------------------------------------------------------
Normalized cuts
In last lecture, we already talked about the segmentation using normalized cuts.
The normalized cuts approach can be formulated as a generalized eigenvector
problem. Here is the summary of the Ncuts approach.

The normalized cuts approach also can be interpolated as a dynamic system,
in which (D-W) is stiff matrix, D is mass matrix and the generalized eigenvectors
are the fundamental mode of oscillation.
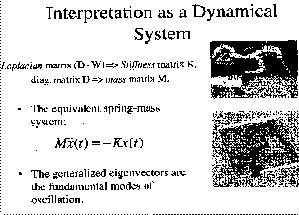
The advantages of the Normalized Cuts approach include:
Factor leading to group
The factors leading to group include:
These factors are reflected in Wij in the Ncuts approach. For example,
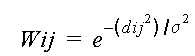
in which dij is the distance between i and j
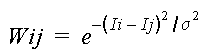
in which Ii, Ij are the brightness of i and j
The combination results can be written as:
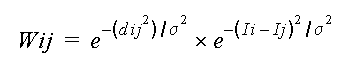
In next section, we will introduce the factor based on the boundaries.
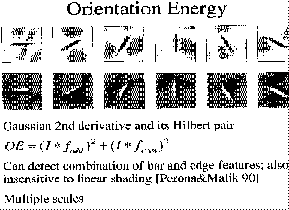
Orientation energy
As shown in the figure, there three point in the figure, P1 and P2 belong
to the same group, the linkage between them is strong. On the contrary,
P2 and P3 are separated by a boundary, the linkage between them is
weak.
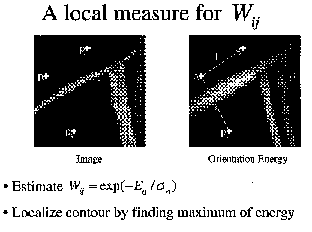
So we employed orientation energy OEij to describe the boundary factor.
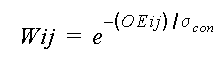
When the orientation between i,j is perpendicular to a boundary, the
orientation energy is large, so the linkage wij will be small. Vice versa
for the orientation parallel to a boundary.
The boundary in a real image is usually a bar, edge or their combination.
See following figure as an example.
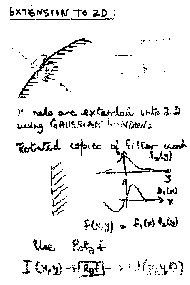
We can use Gaussian filters to detect the orientation energy. We use
the first and second Gaussian derivative filters to detect the edges and
bars. The combination results is the orientation energy. By applying
the filters in 6 directions and multiple scales, we can find the direction
with the maximal orientation energy, which is the direction perpendicular
to the boundary.