Lecture by Professor Malik

Scribe notes written by Wilson Cheng

Date: October 11, 1999 (Monday)

==============================================================================================

From last lecture, we learned:

· Textons are atoms of perception.

· Segmentation using normalized cuts.

· Julesz's textons filter representations.

i) Averages

ii) Marginal histograms

iii) Joint histograms --> ('new' textons)

We understand how to find Wij but how do we find the texture boundaries? We must find textons boundaries and compare them.

Using the Chi Square test:

₂ k [hi(m) – hj(m)]

X (hi, hj) = ½ å ---------------

M=1 hi(m) + hj(m)

₂

Wij = exp (-X (hi, hj) / stex

Review a little bit more about “norm”:

L1 norm |V1| + |V2| + … + |Vn|

_{2 2 2}

L2 norm Ö(V1 + V2 + … Vn )

Linf norm = MAX |Vi|

i

Memo: To get help about normalization in Matlab, type “help norm”

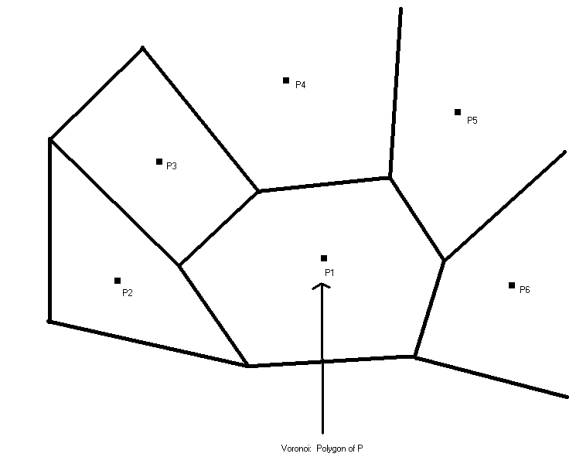
Voronoi Diagram and Delaunay Triangulation

Using an example of post offices as an illustration:

P’s are post offices.

Goto nearest post office, then find the space closest to the next post office

(“Dual” notion of neighbors also known as “dual” representation);

Then compute set of neighbors == Delaunay neighbors

Find average distance by taking the median.

Whether a line is a boundary of another object or it’s interior segments can be tested using the Chi-Square test.

If texture is inside, Chi-Square » 0.

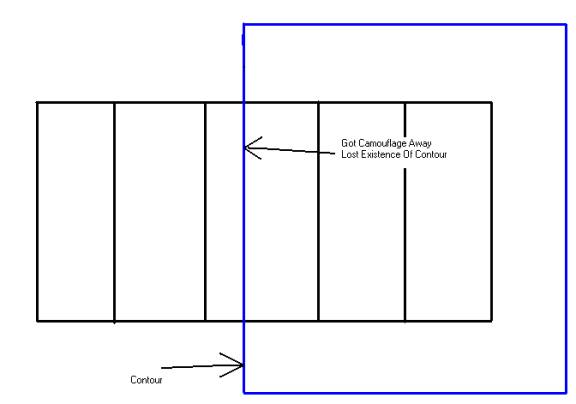
The above phenomenon where boundaries are seen as interior segments is called “crowding”

· Measuring texture similarities by using texton histograms.

Cue Integration

Contour Texture

Wij = Wij * Wij

Gate contour texture cues are based on boundary versus interior test.

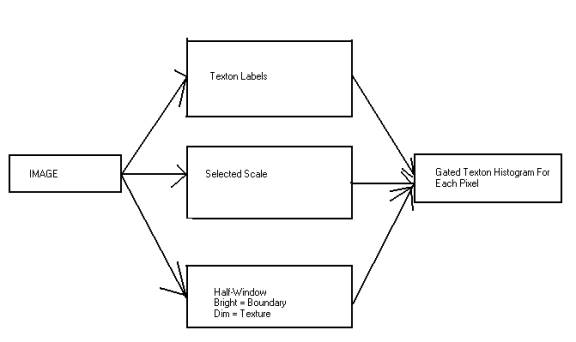
Gating the texture Cue

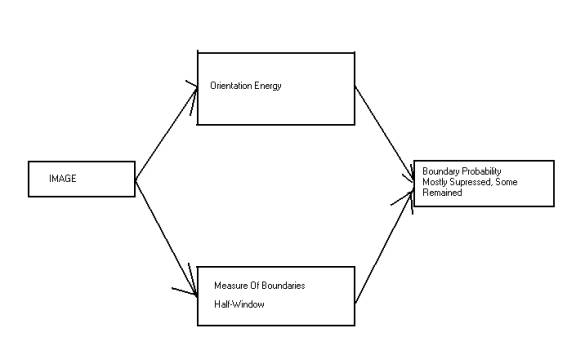
Gating the Contour Cue

Conclusion:

If possible, we should use global analysis for it’s more accurate than local examination. Also combining information from different scientific sources gets you more accurate results.

================= END OF SCRIBE NOTES =================