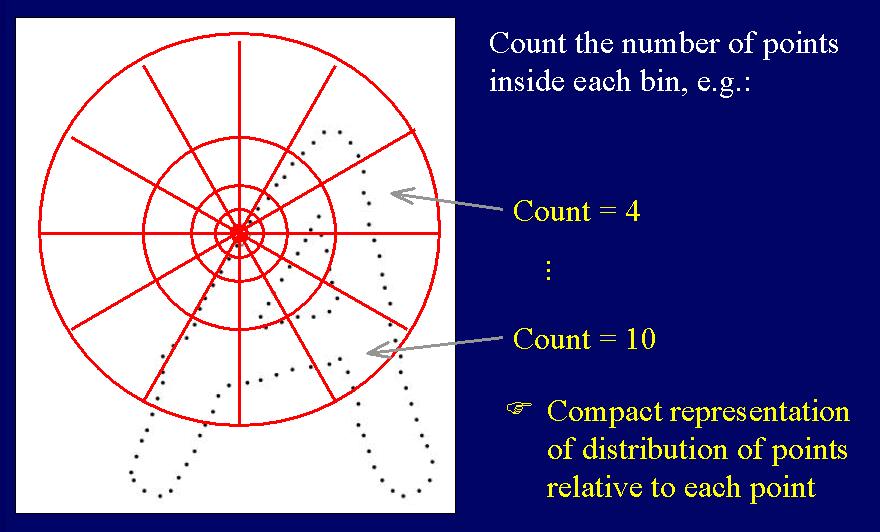
The "shape context" is a new descriptor we have developed for finding correspondences between pointsets. It is described in the following publications:
Our ICCV 2001 paper contains our record-setting handwritten digit results. This is a problem on which many different algorithms have been compared; see Yann LeCun's algorithm comparison list at AT&T, a representative subset of which is quoted in the following table.
| METHOD | TEST ERROR RATE (%) |
| K-nearest-neighbors, Euclidean | 5.0 |
| K-nearest-neighbors, Euclidean, deskewed | 2.4 |
| 40 PCA + quadratic classifier | 3.3 |
| 1000 RBF + linear classifier | 3.6 |
| K-NN, Tangent Distance, 16x16 | 1.1 |
| Virtual SVM deg 9 poly [distortions] | 0.8 |
| Boosted LeNet-4, [distortions] | 0.7 |
The above methods all used a training set of size 60,000. The last two included synthetic distortions of each digit in the training set to produce a training set of size 600,000. Error rates are measured using a test set of size 10,000. Our error rate using shape contexts and a K-nearest-neighbor classifier is 0.63% with a training set of size 20,000.
| METHOD | TEST ERROR RATE (%) |
| K-nearest-neighbors, Shape Context [10,000 training] | 0.71 |
| K-nearest-neighbors, Shape Context [15,000 training] | 0.67 |
| K-nearest-neighbors, Shape Context [20,000 training] | 0.63 |

Thus we get descriptors that are similar for homologous (corresponding) points and dissimilar for non-homologous points, as illustrated here, where the bin counts in the histogram are indicated by the grayshade (black=large, white=small):
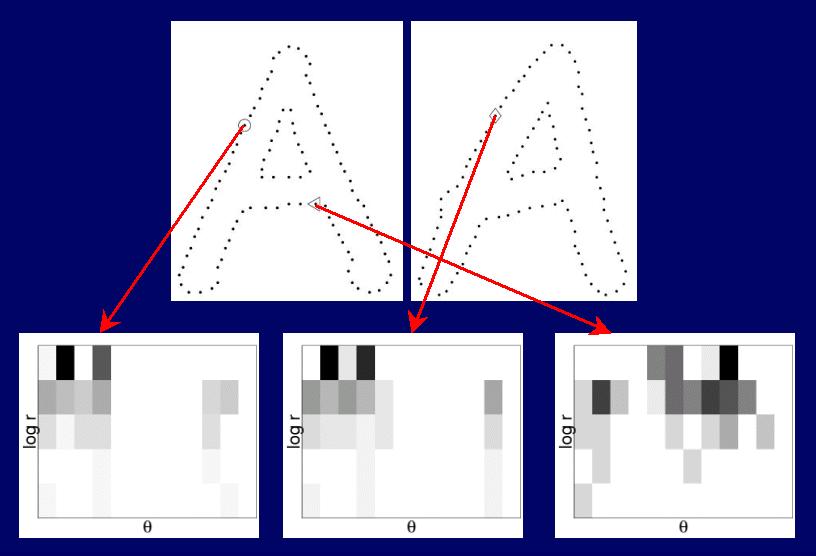
We then use the shape contexts as attributes for a weighted bipartite matching problem.
More to come...